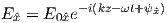
Abstract
Castillo demonstrates an important case of successful superposition of elliptically-polarised light by moving to spinor representations of electromagnetic plane waves: when the angle between the two unit spinors as represented on a Poincare sphere are (as a complex number) either 1, -1, i or -i. This paper demonstrates that there are additional conditions under which superposition is successful: phase-shifting of one of the waves by π∕4 prior to superposition. Two and three superpositions are shown, and the candidate configurations for each are listed. The result is significant for Particle Physics at least, in that Castillo and Rubalcava-Garcia’s prior work show a correspondance between Jones Calculus and SU(2), and gives a direct mapping between Jones and Pauli Matrices.
Let τ = 2π! [6] Superposition of identical frequency elliptically-polarised Jones Vectors may easily be demonstrated to be the sum of the Jones Vectors, in a non-constructive, non-destructive simple fashion if the phase difference between the two is zero or τ∕2. Castillo [5] in equation (34) demonstrates a more general result that includes a phase differential of τ∕4 and -τ∕4, or where, if the vectors are represented as spinors, one vector’s angle minus the other modulo τ∕2 is zero. In these circumstances the vector’s magnitude uses pythagoras in effect to calculate the magnitude of the superposition result.
We show in this paper that there are special circumstances (certain very specific Jones Vectors) that, if one of them is first phase-shifted by τ∕4, will also successfully superimpose and meet Castillo’s conditions outlined in equation (34).
Jones vectors are normally expressed as follows:
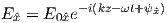 | (1) |
However Castillo and Rubalcava-Garcia’s in [4] equation (7) move them to spinors. Here is Castillo’s equation (34):
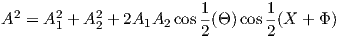 | (2) |
where A is the superposition result E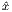 , A1 and A2 are the two elliptical vectors being superimposed, Θ is the
angle about z between the two vectors (including phase delay), X is the phase of A1 and Φ is likewise the phase of
A2.
, A1 and A2 are the two elliptical vectors being superimposed, Θ is the
angle about z between the two vectors (including phase delay), X is the phase of A1 and Φ is likewise the phase of
A2.
First we will show superposition conditions of two elliptically-polarised plane waves, and once that result is achieved we then demonstrate three.
The key is that we are looking for conditions where either Θ is zero or X + Φ modulu τ is zero. From intuition and symmetry we suspect that a phase shift of 6∕12τ is the key. First however we must derive an equation similar to 2 except incorporating a phase-shift. From section 3.1 of [4] a rotation of δ is equivalent to multiplying by e-iδ∕2. If we then apply that to A2 the end result is:
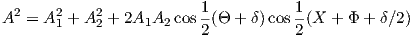 | (3) |
Note that whilst the angle between the two has been increased by a factor of δ, the tangent vectors have been separated only by a factor half that amount. This is very important as we will see, later.
Two known candidates which have been noted to successfully superimpose are when X = τ∕12 and Φ = 2τ∕12. In our first attempt, Φ now has been phase-shifted by an additional 3τ∕12, and Θ by 6τ∕12.
Substituting these into equation 3 we get:
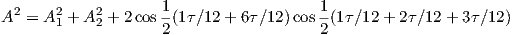 | (4) |
With X + Φ + δ∕2 equal to 6∕12τ, this satisfies Castillo’s conditions because cos(3∕12τ) is zero. Thus, we demonstrate that two monochromatic elliptically-polarised waves of angle 1∕12τ and 2∕12τ may successfully superimpose if the second has its phase advanced in relation to the first by exactly 3∕12τ, which happens when the second wave is shifted forward by 6∕12τ. There are four other such positions that may easily be demonstrated to also superimpose by rotating both waves by multiples of 3∕12τ. The cases where the first angle is opposite to the second were already demonstrated to superimpose through Castillo’s original work: these are where each wave is a mirror-image along either the real or imaginary axes.
Intuitively we may view this as being a naturally-expected result: firstly these are two waves being superimposed, so having to offset one of them by 180 degrees should not be too much of a shock. The second part is that the resultant superposition’s vector may be viewed as being the vector between the two end-points of the contributing vectors, after one of them is rotated by 90 degrees. Thus the superposition is in effect the completion of an equilateral triangle. This is an important insight that becomes relevant for triple superposition.
From an independent source it is suspected that there exist precisely a total of sixteen potential candidate triple-superpositions which fit the above derived rules. The actual number of permutations of 1∕12τ subdivisions would seem to make a total of 312 candidates, however the rules above need to be applied (and satisfied) a total of four separate and distinct simultaneous times:
The number of combinations is therefore extremely rapidly narrowed down. The key selection criteria is that the Jones Vectors must (prior to even attempting to carry out the confirmation) is to eliminate anything where the constituent vectors do not sum to one of the four "compass" points in the imaginary plane: 1, -1, i or -i. or where they sum to one of the other source vectors, thus forming a Group. This criteria alone turns out to be sufficient to eliminate all but sixteen permutations (sixteen more being mirror-images of the same) - see Table 1.
It is worthwhile noting that the mirror-images also form a Group, where the overlap between the two Groups is solely on the major compass points. Also, we may wonder why there are no permutations such as for example 10/12 2/12 n/12 but from the above 2-superposition section we can conclude that the reason why there are no 10/12 2/12 permutations is because the distance between the end-points of 10/12 and 2/12 do not make a unit vector. Put another way: only those candidates which somehow involve an equilateral triangle are possible.
So after successful use of 6∕12τ we might guess that with three waves to superimose, a phase offset of 8∕12τ would work. Looking at the first entry in the table, we choose to leave the first entry where it is, phase-offset the second by 8∕12τ and phase-offset the third by -8∕12τ.
Taking the first and second wave, we set X = 1∕12τ, Φ = 8∕12τ (to be phase-shifted by 4∕12τ). Θ which was formerly 7∕12τ (the difference between X and Φ) is phase-shifted by 8τ∕12. Substituting these into equation 3 we get:
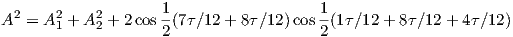 | (5) |
Surprisingly, this doesn’t work. Instead, we try 6∕12τ for the second wave. Taking the first and second wave, we set X = 1∕12τ, Φ = 8∕12τ (to be phase-shifted by -3∕12τ). Θ which was formerly 7∕12τ (the difference between X and Φ) is phase-shifted by -6τ∕12. Substituting these into equation 3 we get:
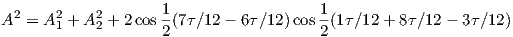 | (6) |
Now we have the second cosine equal to zero. Let us now try wave 2 and 3. Let X = 8∕12τ (to be phase-shifted by -3∕12τ), Φ = 1∕12τ (to be phase-shifted by -3∕12τ). Θ which was formerly -7∕12τ (the difference between X and Φ) is phase-shifted by -6τ∕12 for X but an additional -6τ∕12 for Φ (which cancel modulo τ). Substituting these into equation 3 we get:
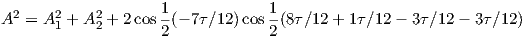 | (7) |
Surprisingly this doesn’t work. Instead, let’s try -6∕12τ for wave 3, leaving wave 2 offset by -6∕12τ. Let X = 8∕12τ (to be phase-shifted by -3∕12τ), Φ = 1∕12τ (to be phase-shifted by -3∕12τ). Θ which was formerly -7∕12τ (the difference between X and Φ) is phase-shifted by -6τ∕12 for X but an additional -6τ∕12 for Φ. Substituting these into equation 3 we get:
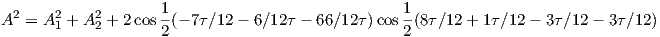 | (8) |
Fascinating. It would seem that a phase retardation of 180 degrees has to be applied to both waves, resulting in both X and Φ being retarded by 90. Let us last check wave 3 and 1.
Let X = 1∕12τ (to be phase-shifted by -3∕12τ), Φ = 1∕12τ. Θ which was formerly 0∕12τ (the difference between X and Φ) is phase-shifted by -6τ∕12. Substituting these into equation 3 we get:
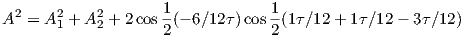 | (9) |
Here it is the first cosine that is zero, instead of the second, due to them being identical but one rotated by 180 degrees. Thus we have shown that three pairs of waves individually superimpose with each other. The triple superposition is beyond the author’s current ability to assess, attempts leading to incorrect answers. Logically however it is reasonable to expect that if 1 superimposes with 2, 2 superimposes with 3 and 3 superimposes with 1, then 1, 2 and 3 also superimpose. It would be nice to have confirmation of that, because finding out the sum of the three Jones Vectors is in itself an important mathematical result. It would also be nice to generalise the above: we expect the result to be that the required phase offsets is identical for all sixteen (thirty two) waves.
The author was genuinely anticipating to be demonstrating that the required phase offsets were to be 8∕12τ so as to create equilateral triangles, because it was believed that the rotations would additionally offset each wave so that they would fit together at 60 degrees, neatly. However, from the independent source which is an extension of a well-known particle physics theory, the result that the phase offsets are 6∕12τ thus rotating the vector’s angles by half that amount, is also an expected result, just in a different area of the theory.
It does however make much more sense for the phase offsets to result in the superpositions being orthogonal, as that would mean that each wave’s real and imaginary parts would not interfere with each other at any time, thus creating the very conditions necessary for non-constructive, non-destructive superposition outlined in Castillo’s paper [4].
We note also that braiding order is important and has been demonstrated to be preserved [2]. In the light of the above superposition result, preservation of braiding order begins to make sense. Also we note Bekenstein and Kaminer et al’s efforts to superimpose gaussian beams to as to remain self-phase-coherent [3]. We suspect that here, again, the phase-coherent solutions that they found would fit the superposition criteria noted here.
Lastly in summing up from the extension to the well-known particle physics model that inspired this investigation, we note that if Bekenstein and Kaminer’s work results in a circular loop (which in other theoretical work they successfully show), or if we may assume a Friedmann-Robertson-Walker spacetime of size identical to the wavelength of the waves being superimposed, that whilst from the perspective of the elliptically-polarised plane waves they would appear to be travelling on a straight line in cartesian coordinates, the fact that such waves would in effect be in a curved, looped universe of exact circumference to fit their exact wavelength, we literally have defined the exact conditions for photons to be the constituents of a particle.
Isaac Freund, Multi-twist optical Mobius strips, arxiv:0910.1663, 9 October 2009.
http://arxiv.org/abs/0910.1663
[2] Thomas Iadecola, Thomas Schuster, and Claudio Chamon, Non-Abelian Braiding of Light, DOI:10.1103/PhysRevLett.117.073901, arXiv:1509.05408, 10 August 2016
http://phys.org/news/2016-08-physicists-method-braiding.html,
[3] Rivka Bekenstein, Jonathan Nemirovsky, Ido Kaminer and Mordechai Segev, Nondiffracting Accelerating Wave Packets of Maxwell’s Equations, doi:10.1103/PhysRevLett.108.163901, 6 April 2012.
G.F. Torres del Castillo and I. Rubalcava-Garcia The Jones vector as a spinor and its representation on the Poincare sphere, arxiv:math-ph/1303.4496, 19 March 2013.
http://arxiv.org/abs/1303.4496
G.F. Torres del Castillo Spinor representation of an electromagnetic plane wave,
J. Phys. A: Math. Theor. 41 (2008) 115302 (8pp), doi:10.1088/1751-8113/41/11/115302