Copyright (C) 2017 Luke Kenneth Casson Leighton. All Rights Reserved
Contact: lkcl@lkcl.net Date: 06 Jan 2017
Ref: Revision: v1
In a prior paper [1] ultracolour was added back in to the Extended Rishon Model, and the
I-Frame structure explored using the proton as an example. Bearing in mind that because Maxwell’s
equations have to be obeyed, the Rishons have to have actual phase, position, momentum and
velocity. The only pattern of motion that fitted the stringent requirements was if the Rishons
circulated on mobius strips. Fascinatingly and very excitingly, exactly such a previously-theoretical
elliptically-transverse mobius topology of light [4] has been experimentally confirmed last year [3].
The next logical task of writing out Rishon triplets in a circle as actual starting phases of the
elliptically polarized mobius-walking light has proven to be a huge breakthrough, providing startling
insight with massive implications such as implying the existence of two previously undiscovered
quarks very similar to up and down (provisionally nicknamed over and under), logically and
naturally confirming that "decay" is just a "phase transform", and generally being really rather
disruptive to both the Standard Model and the Extended Rishon Model.
A huge task is therefore ahead, to revisit the available data on particle decays and masses (bear
in mind that the Standard Model’s statistical inference confirmation techniques assume the up
and over, and down and under, to be the same particles), so this paper endeavours to lay some
groundwork and ask pertinent questions.
Contents
1 Introduction
I have to start by admitting that I’ve never been so excited and so annoyed at the exact same time in
discovering new information or insights, before. Both have occurred mutually exclusively, but never at the
same time. Excited because the hypothesis that Rishon Triplet colour, makeup and layout is simply the
relative starting phase of an elliptically polarised mobius-looped phased gaussian array of photons fits (and
vindicates) thirty years of work, but incredibly annoyed because not only has the Standard Model completely
missed the possibility of there being two undiscovered quarks (over and under), but so did I. That means that
a complete overhaul of the Extended Rishon Model is needed, where the available data has and every
other theoretical physicist has also missed them. I therefore have to be really, really sure about
this.
Taking one step at a time however, I outline the Rishon triplets on a phase diagram (circle) then show,
through some examples, the changes (simplifications) that need to be made to the Extended Rishon Model
rules, as well as those of phase transforms ("decay"). A preliminary analysis is done into the
significance of the undiscovered phase positions indicative of the two new quarks, over and under.
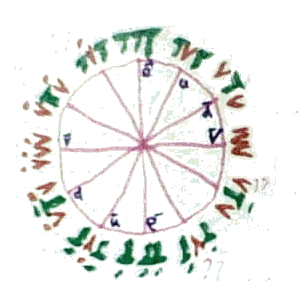
Figure 1: Twelve Rishon positions, 4 unidentified
2 The 12 phase diagram
Let τ = 2π! [14] In the paper in which I explored hypercolour [1] I arbitrarily laid out the proton as
below and concluded that if all three quarks were following parallel mobius strips, the Rishon triplets would
represent phases.
 | (1) |
This led me to the sudden realisation that the Rishon triplets must simply represent the phase (I,Q) on a
full τ revolution in complex space, i.e. that they really would be transverse photons on a mobius strip, exactly
as demonstrated experimentally last year [3].
What I didn’t know was what the phase angle actually was. Bear in mind that I was assuming that there
were only eight Rishon triplets, that the "rules" of the Extended Rishon Model only permitted eight Triplets.
So, naturally, I tried laying out the triplets in a circle, separate by 45 degrees: they didn’t fit. TV T cannot be
made to line up 180 degrees opposite to V TV if we also expect the electron to be 180 degrees lining up
opposite the positron. The breakthrough therefore was to lay them out separated by 30 degrees (τ∕12), as
shown in figure 1
Immediately the symmetry caught my attention, as did the puzzle of the extra four unidentified phases at
4τ∕12, 5τ∕12, 10τ∕12 and 11τ∕12. However before exploring that, I noticed that T, if we assume it to be
"real number", matched perfectly with the phases (going negative in the second half) and likewise, exactly
τ∕4 out of phase, if we were to assume it represented a "complex number", V correspondingly matched. Bear
in mind that, in the previous paper, I had just done a rotational analysis which showed that two up quarks
remained perpendicular to down at all times, as long as a transverse mobius circuit may be
assumed.
Excitedly, I checked the VT0-paired phase transform "rules" from my notes, identifying those quarks which,
from phase-transform (aka "decay") analysis I had derived four years earlier, and marked the triplet-pairs
(phase-pairs) that are permitted to transform to any other triplet-pair (including positional interchange i.e.
swapping places with each other in any given particle), marking V T0 in pink and V T0 in purple, below:

Figure 2: VT0 Phase Transforms
The key thing which is very exciting here is that the VT0 transform pairs are all separated by 5τ∕12 (just
in a different direction for each type of VT0 transform) and the two quarks that make up a gluon (aka
"ultra-ultra-short-lived-pion") are separated by 1τ∕12. So, immediately, I wondered if there was a refinement
of the VT0 phase transformation rules, that only transforms are permitted that flip exactly 1τ∕12 (30
degrees) rather than, as previously surmised, a jump which represents 60 degrees is in fact "permitted". This
is going to need careful investigation.
But even before that, I wondered "what the heck is at 4τ∕12 and 5, 10 and 11? Because if we consider
these to be simply different starting positions of Freund’s multi-twisted elliplically-polarised mobius-strips [4],
there’s absolutely nothing that would prevent or prohibit the occurrence of those phases by nature: Maxwell’s
equations have to be obeyed... period.
Also, I have to relay that I initially made the mistake (repeatedly) of thinking that a single photon would
fit the model: it doesn’t. Freund very kindly explained it to me: a photon has a vector, so it is different when
rotated through 180 degrees from its orientation at 0 and 360. Elliptical polarisation is an axis so is a line
not a vector. The exact significance of this is still a little beyond me, but I am "going with it" for
now.
2.1 Spot the deliberate mistake...
The first thing to observe about Figure 1 is: I’ve placed the up and down quark nomenclature against the
Rishon triplets that I believed to be correct according to the Extended Rishon Model... but that rather
unfortunately puts up and down at 5τ∕12 instead of at 90 degrees (3τ∕12), and from the I-Frame layout and
the prior "rotational" exercise we deduce this to be wrong.
argh.
The correct position for the up quark would be at 10τ∕12. Now we need to re-verify all of the phase
transformations in light of this new information... bear in mind that there’s the strong possibility
that some of the particle "decay" patterns from which the Extended Rishon Model’s rules are
deduced might actually be over and under quarks, and the problem quickly becomes a bit of a
handful.
So, beginning that process I laid out the Rishon triplets again (reverting once again to Haim Harari’s original
sign for the Vohu Rishon [6]), and quickly realised that the 5τ∕12 relationship was going to be unavoidable:
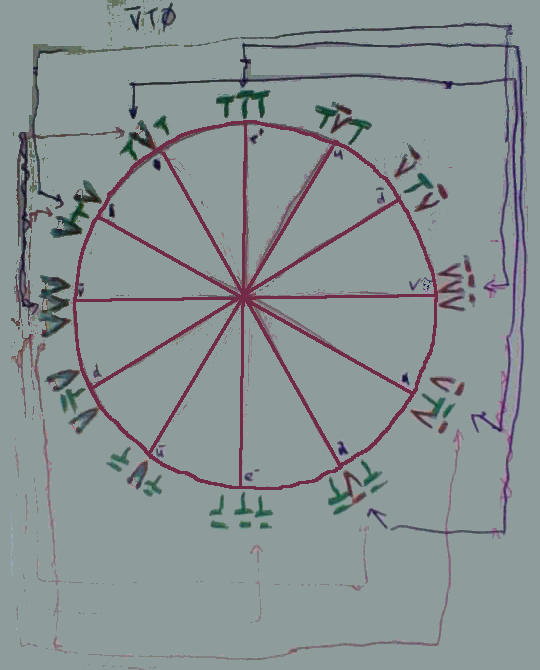
Figure 3: 12 Rishons, inverted Vohu (imaginary)
Once again, frustratingly, when walking by hand through the sum of T and V particles, very quickly it
became apparent that if the proton is now made up of (TV T,V TV ,TV T) the pions still have to be
made up of quarks that are 1∕τ apart. In short: it just doesn’t work. Not only that but whilst T
increases and decreases in a clockwise direction, V increases and decreases in an anti clockwise
direction.
I did however have the opportunity to analyse the VT0 phase transforms again, and discovered something
quite interesting:
∙ The up, down, electron and neutrino triplets are separated by matched V T0 and V T0 phase
transforms
∙ The over, under, electron and neutrino triplets are separated by V T0 and V T0 phase transforms
(same-sign per transform)
∙ Constructing a pion from over anti-under or under anti-over would still obey the rules of integer
(1 or -1) Vohu and Tohu, but that when compared to the corresponding pion+ and pion-, the
sign of the sum total Vohu would be inverted.
∙ The V T0 (and opposing) transformations cannot be applied to the up and down quarks, just
as V T0 and V T0 cannot be applied to over and under.
These observations still apply to the originally-chosen orientation of Vohu’s sign. This latter observation is
where we might begin to be getting some insight as to why over and under have not been detected, or
that if they have, they’re part of a kind of "mirror set of decay patterns" which are in effect
near-indistinguishable from the corresponding phase-transforms, apart from potentially a small mass
discrepancy.
The real answer may turn out to be much more straightforward, given that we’re talking about Maxwell’s
Equations here, and talking about electro-magnetism. It could simply be the case that the over and under
quarks, by virtue of the inverted Vohu sign, are oppositely-magnetic and thus where we would expect the
"normal" particles to attract, they simply repel instead. So it may turn out to be the case that far from ever
expecting to see existence of over and under quarks in the wild, the complete opposite is the
case!
All that aside: we still have to point out the mistake that was spotted which turns out not to exist, in
relation to the up-down-up layout of the proton.
2.2 ...which turned out not to be
My initial objection to the fact that up and down are separated by 5τ∕12 was that this could not possibly
stabilise three quarks at 90 degrees (3τ∕12) phase-differential, which we now appreciate to potentially represent a
stable non-interfering E.M. relationship between three ellipcically-transverse mobius beams on their circular orbit.

Figure 4: Proton Mobius stack)
Then I remembered what I had done: when at a restaurant entertaining some young children, I had made
three mobius strips out of paper. When they tired of playing with them, it was my turn, so I tried to stack
them together in a similar arrangement to that which I had described in my previous paper [1]. The only
arrangement that "fitted" was if:
∙ the two "up" mobiuses were twisted slightly through 45 degrees
∙ the central "down" mobius was twisted slightly through -45 degrees
∙ the central "down" mobius was turned upside-down (rotated about the X-axis by 180)
∙ the central "down" mobius was rotated about the Z axis through an entire 180 degrees compared
to the two up strips.
Then and only then did the angle at all times of the three strips line up exactly at 90 degrees to each
other as outlined in the "stages" of the previous paper when starting from that initial I-Frame setup. Thus,
the fascinating point is: the rotation by 180 degrees of the middle (down) quark about the X-axis
mirror-images the up quark’s relative angle when compared to the two up quarks (whereas the Z-axis
rotation just shifts the phase by τ∕2), and the combined effect of the two 180 degree rotations
bring it back into sync so that the three quarks all travel together in the same orbit about the Z
axis.
I find this to be absolutely fascinating, that there would happen to be an exact corresponding
arrangement of elliptical transverse polarised arrangements of light that happen to match the I-Frame
rotation, which happens to have been deduced from a comprehensive analysis of particles.
So now I had to come up with a way to map these paper-and-pens proton experiments back to the
I-Frame representation in a way that made sense. My primary objection - from O-Level physics - is the
"right-hand motor rule" must be obeyed: "First-finger field, middle finger current, thummmmb-motion". It
basically tells me that at all times the three Rishons (aka elliptical polarisation axis) need to be at right
angles.
So I tried adding the Rishon values up: no dice. I tried treating the Rishons as vectors: no dice. Then it
hit me: of course, this is complex numbers: you multiply and divide them! Which means simply adding and
subtracting the angles. So from figure 3, take the (starting) position of the up quark - -1τ∕12 - and subtract
it from the (starting) position of the down quark - 4τ∕12. We now have 3τ∕12 which is a 90 degree angle and
I’m happy at last, because that’s finally an explanation as to why the Rishon I-Frame is laid out as it
is.
This is rather hard to see in figure 4, not least because it’s not possible to show the axis-inversion which
actually occurs in elliptically-polarised light: for that you have to go to Bauer et al’s paper [3] and examine
figure 2(b). They’ve very kindly laid out two examples (C1 and C2) which happen, apart from the starting
angle needing to be shifted by -1τ∕12, is pretty much exactly the up and down quark respectively. We can
surmise that the up quark will be the one that starts primarily in the real numberplane (primarily electrical
presence) and the down quark in the complex.
One last thing: if you add (superimpose) all three fields, the sum total angle comes to 6τ∕12 (a
real number, -1): it’s not the right sign for a proton (should be +1) but one step at a time,
eh?
2.3 Analysing additional particles and phase-transforms
To be able to do phase-transforms we need the pion. Let’s take the π+:
 | (2) |
Subtracting the phase angle of these two quarks equals 1τ∕12 (which explains why they’re not stable) but
adding them we get 3τ∕12. This is slightly different from our initial supposition (where the sum
total number of separate V and T was required to add up to integer 1, 0 or -1) but it’s actually
much simpler and, in light of the recognition of Rishon triplets being phases, makes a lot more
sense.
We could also do the same thing here for any of the other quarks (including over anti-under), but the
main point’s been made: subtraction and addition of the phase-angles that the triplets represent are not both
on a compass-point for any combination which makes up a pion (unlike the electron and neutrino, which
already are, and the proton and neutron, which by a nice mathematical coincidence fit onto the compass
points). Neutral pions, obviously being comprised from quark-anti-quark would, if the two quarks represent a
superposition of opposite-phased elliptically-polarised mobius light, obviously result in cancellation aka
"anti-matter explosion" which gives us a rational explanation as to why we don’t see any stable particles in
the pion-0 family.
Phase transforms (aka "decay") involving the W and Z Bosons are so fantastically
laborious that it’s best to start with a simple example first of all: pion+ "decay":
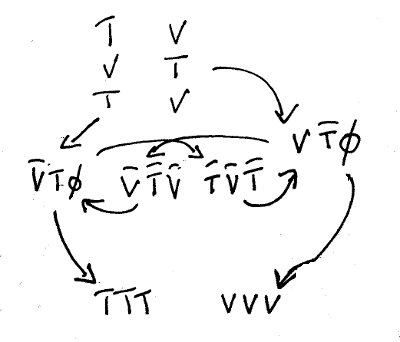
Figure 5: Simple Pion Phase Transition
The "gluon" - which I re-classify in light of the insights from the Extended Rishon Model as a "pion that
get’s created and destroyed pretty much instantly" - we can now understand to be a superposition of two
more phase-angles that, again, happen to be separated by 1τ∕12 and happen to sum up to a compass point
(1, i, -1, -i).
Now within the framework of elliptically-polarised phase-ordered light, the prior "rule" that particles
must be made in combinations, the sum total of which must come to zero - summarised as "the universe does
not just create "charge" out of thin air" - begins to make sense. Re-evaluating the V T* rule in light of
phases, it may be written as "four Rishon Triplets may only materialise out of thin air if the sum total phase
is a zero-sum game". We also surmise that it’s simply too challenging (too much energy required) for the
universe to pull up electron, positron, neutrino and anti-neutrino out of "thin air", preferring
instead to go via the intermediaries of the compass points in between the major N, S, E, W
ones.
Returning to the pion phase transform: I suspect that due to this being the pion+ that’s "decaying", and
it needs a pion- to complete the transition, the "resonance" conditions are right there already, making the two
pions sort-of their own "VT*". It feels like a bit of a cheat, but when you think of it in terms of
superimposition of the phases, it makes sense.
To take an analogy, here: take two sources of light that can generate Red, Green and Blue. Make one
source shine Red light, and the other Green-plus-Blue light. Now shine both sources onto the same spot:
what do you get? You get white light of course. Now change the intensity of source 1 so that it
includes green light and at the exact same time and by the exact same amount decrease the
intensity of the Green in source 2. Keep shining the two sources onto the same spot: can you tell
if anything is happening? No of course not, because the sum total is still white light. At the
point at which source 2 becomes entirely only Blue, move them away: you’ve just interchanged
the Green from source 2 to source 1 without anyone being able to tell. Something remarkably
similar is going on with the VT phase transforms, that extends all the way up to the W and Z
Bosons, which I determined from comprehensive analysis to be made up simply from... more
pions.
3 Discussion
The original Extended Rishon Model rules were based on numerical values, so naturally it felt right to sum
them up. Surprisingly, when moving to the complex numberplane represented by twelve equidistantly-spaced
points along e-iτω, 0 <= ω < 1, the rules still work and remain intact, with the notable exception of the pion
being that the superposition (sum) of its phases is on a major compass point, not as we previously surmised,
V=+/-1 and simultaneously T=+/-1. This also makes much more sense: a particle with sum-total 1
magnetic, 1 electrical magnitude charge (as opposed to 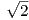 of the same) just doesn’t feel quite
right.
of the same) just doesn’t feel quite
right.
Also we have a natural explanation as to why the I-Frame "works": the two outermost Rishon triplets
are exactly 3τ∕12 apart, and, if a particle is to be stable, the sum total (superposition) of all
Rishons phase again must come to a major compass point, which represents either electrical
charge +/-1 or magnetic charge +/- 1. This is why the proton (and neutron reasonably so) are
stable.
We also note that:
- Carl Brannen and Marni Sheppeard were the first to notice that π∕12 is involved in advanced
mass analysis (extended Koide relationships) [8]
- Zenczykowski’s Equation (14) in phase-space is also of the form e-iτ [9] but that there is no
actual enumeration of the phases as fractions that would allow them to be identified in the way
outlined in this paper
- Freund’s equation 1 [4] being based on gaussian beams also includes e-iω
- Jay Yablon’s work on mass-fitting (yang mills monopoles) uses a gaussian ansatz to gain
incredibly-accurate mass predictions [11]
- that the de Vries formula includes a factor e-τ∕4 which we consider to be highly significant [13]
I feel compelled to mention that I am deeply saddened by the mainstream reactions towards anyone that
puts forward a hypothesis, or references work from the earlier half of the 20th Century, which summarises as
"electrons are photons in mobius strips". Both mainstream scientific forums where such ideas were put
forward were censored, with several people stepping forward to vilify the moderator for his actions, until he
simply closed all comments [5]. It is noted with some anger that the moderator recommended that readers
simply "close their minds" to any views that they disagreed with (just as the moderator himself
did).
The role of a scientist is not to be judgemental. Certainty is a pathological state of mind! I cannot ignore
the overwhelming evidence stacking up and will continue to explore until someone provides proof that the
hypothesis under exploration is wrong. That’s stacking up to be quite a lot of circumstantial
evidence.
Open questions still to be investigated:
- Is it really this simple?
- What is the relationship (if any) between the de Vries formula and equation 4 of Freund’s paper
[4]?
- Is it really as simple as being that the Rishon triplets "superimpose" one over the top of the other
to create compound particles, or do the fields generated by the elliptically-polarised mobius-strips
keep each other separated by some distance? Bear in mind that braided light is possible [10] so we
consider it reasonable that the superposition of mobius strips would not result in the destruction
of the strips, except where the phase differential is sufficiently close to cause "decay".
- How the heck can the up and over quarks be discerned from each other, likewise down and under?
- Is the elementary charge simply the influence of the elliptical polarization effect of the
mobius-strip light?
There is so much here that needs to be investigated it’s overwhelming.
References
[1] Luke Kenneth Casson Leighton, Exploring the Addition of Hypercolour to the Extended Rishon
Model, vixra:1701.0290, 03 Jan 2014.
http://vixra.org/abs/1701.0290
[2] Luke Kenneth Casson Leighton, A Discourse on the Electron and Other Particle’s Internals,
from the Perspective of the Extended Rishon Model and the Field of Optics, vixra:1701.0016, 03
Jan 2014.
http://vixra.org/abs/1701.0016
[3]
Thomas Bauer, Martin Neugebauer, Gerd Leuchs, and Peter Banzer Optical Polarization Mobius
Strips and Points of Purely Transverse Spin Density, arxiv:1601.0607, January 25, 2016
http://arxiv.org/abs/1601.06072
[4]
Isaac Freund, Multi-twist optical Mobius strips, arxiv:0910.1663, 9 October 2009.
http://arxiv.org/abs/0910.1663
[5]
http://physicsworld.com/cws/article/news/2015/jan/29/how-to-twist-light-into-a-mobius-strip
[6] Harari, H. (1979). A Schematic Model of Quarks and Leptons, Physics Letters B 86 (1): 83–86.
Bibcode:1979PhLB...86...83H. doi:10.1016/0370-2693(79)90626-9.
[7] Luke Kenneth Casson Leighton, An introduction to the Extended Rishon Model,
vixra:1403.0016, 03 March 2014,
http://vixra.org/abs/1403.0016.
[8] C A Brannen, Koide Mass Equations for Hadrons, vixra:0904.0006
http://vixra.org/abs/0904.0006
[9] Piotr Zenczykowski (2008), The Harari-Shupe preon model and nonrelativistic quantum phase
space, arXiv:hep-th/0803.0223
[10] Thomas Iadecola, Thomas Schuster, and Claudio Chamon, Non-Abelian Braiding of Light,
DOI:10.1103/PhysRevLett.117.073901, arXiv:1509.05408, 10 August 2016
http://phys.org/news/2016-08-physicists-method-braiding.html,
[11] Jay R Yablon, Why Baryons Are Yang-Mills Magnetic Monopoles, vixra:1211.0151, January
2013 in Number 4, Volume 35, 2012 pp 401-468 of the Hadronic Journal.
http://vixra.org/abs/1211.0151
[12] J.G.Williamson, On the nature of the photon and the electron, DOI:10.1117/12.2188259,
September 15.
[13] Luke Kenneth Casson Leighton, An explanation of the de Vries formula for the Fine Structure
Constant,
http://vixra.org/abs/1701.0006, DOI:vixra:1701.0006, 02 Jan 2017.
[14]
https://tauday.com/tau-manifesto







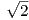 of the same) just doesn’t feel quite
right.
of the same) just doesn’t feel quite
right.