Next: Further observations on phase Up: Decay Patterns as Phase Previous: Summary from example phase Contents
Kaons are basically Pions with a heavier (I-Frame) quark in one of the two spots. That makes them particularly unstable as a rotational unit, and it results in some unusual transitions. Additionally, some anomalies have been observed - deviations from the other examples shown above. Beginning with a standard K- decay into a Pion-0, electron and anti-neutrino:
The diagram below shows the same equation in terms of Rishon VT0 phase transitions:
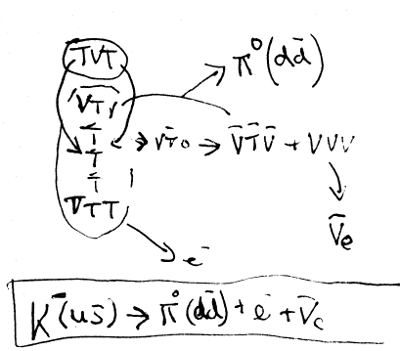figurePotentially over-simplified (perhaps correct?) Kaon decay
|
There are three things wrong with this picture. First is that the up quark phase-shifted with the middle triplet of the anti-strange. As the middle particle (an electron) is almost 2/3s of a match with the up quark - i.e. it comprises two T particles whilst the electron contains three opposing-charged T particles - it almost makes sense for this phase-shift to occur. The problem is: it's only a single phase-shift. Thirdly, one of the particles (the VTV) "jumped" unscathed out of an I-Frame.
Where has the energy required to create this phase-shift come from, if not from another opposing phase-shift? One possible explanation could be that the energy is emitted as a small amount of gamma radiation, whilst the other is that the energy is transferred into the momentum of the remaining particles. The other possible explanation is that the rule about VT0 transfers needing to occur in pairs is simply wrong, which somewhat throws the entire theory here into question.
However, let's look more closely and logically at the options, based on the constituent parts. An up quark - comprising TVT - is orbiting around three triplets in an I-Frame configuration, where the two end triplets are too disparate in their composition for a phase transition to occur. Like pions, Kaons are an unstable two-body rotational entity, so there is nothing to stop the up quark from getting too close to that central triplet (an electron). Once that up-quark and electron phase-shifted into a down-quark and an anti-neutrino, there would be nothing to hold the triplet together. The electron would spin off on its own.
However, let's look carefully at the relative rotation of the remaining particles. The remaining triplets are a neutrino, anti-down quark and now a down quark, where the down quark is rotating about a completely different axis, exactly at right-angles to the anti-down quark that it would ordinarily combine with to create a Pion-0. By the time the transition has occurred, the neutrino from its perspective (and distance) sees two perfectly-balanced quarks (down and anti-down) and thus is not attracted or repelled by them: like the electron it is free to continue on its trajectory.
This just leaves the down and anti-down quarks to resolve the problem of their rotation being at right-angles whilst simultaneously being in extreme proximity to each other. what happens? Is it unreasonable to surmise that there is an additional phase transition that transforms the rotational direction of one of the quarks such that it precisely matches the rotation of the other? Is it unreasonable to further surmise that this transformation precisely matches the energy of a VT0 phase change? How would this be verified experimentally? If it were possible to note (or infer) the momentum, direction of travel as well as the rotation of both the original K- and all the decay particles, it might be possible to confirm, from enough such observations, that the rotational axes can be predicted.
If this were expressed in matrices at all (note: which is beyond the author's mathematical ability to do), then it would be reasonable to include the rotational axis (angular momentum) of the triplets as part of the matrix, not least because that would be critical to explaining how I-Frame triplets hold together in the first place.
However, there may be a simpler explanation - one that holds together under the rules observed so far. Recall the simpler Pion+ decay to a positron and a neutrino. A Pion- would decay likewise to an electron and an anti-neutrino. The difference between the Pion- and a Kaon- is that there is an anti-strange quark present instead of an anti-up. An anti-strange quark is an I-Frame comprising an anti-up, a positron and an electron.
The key to solving the conundrum above - that VT0 phase shifts must occur in pairs - is therefore to use the "trick" that the charged Pions also deploy.
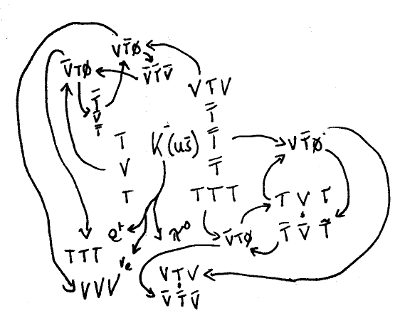figureKaon- decay to Pion-0, electron and neutrino
|
This diagram requires some explanation! The K- is in the centre, with the up quark left of centre and the strange quark to its right. Recall exactly as with the Pion+, the working hypothesis is that the presence of the K-, being unstable, would cause a temporary anti-particle (anti-down plus an up quark) in this case a Pion+ to be temporarily brought into existence. These two particles are shown in the top left corner (at right-angles to each other) just next to their corresponding anti-particles (TVT and VTV) that they will help phase-shift. However the existence of that anti-particle would be not only the output but also the input to a matched pair of VT0 phase-changes. These two matched phase changes are drawn in the top left corner. The output of each of these two? Exactly as with a Pion decay: TTT and VVV Rishons, i.e a positron and a neutrino.
On the opposite side, a similar decay process occurs but this time with a Pion-0 being brought temporarily into existence: again, the quark-antiquark pair (in this case up and anti-up) are both the input and output of a matched pair of VT0 phase transforms. In this way, a positron and an electron transform into a down and anti-down pair: a Pion-0.
With a little more work, by examining and copying the more complex (more common) Pion decay pattern it is easy to see how a Kaon- could decay into a Muon and Muon Neutrino, by virtue of the up and strange particles first being transformed into a W- Boson.
Additionally, the sorts of oscillations that B-Mesons undergo, as simple phase-shifts, can also be demonstrated just as easily to apply to Kaon-0 and Pion-0 particles.