Next: Possible stable anti-muon / Up: Quarks and other Elementary Previous: Rishon colour Contents
Much earlier in this paper the issue was raised of how 9 Rishon I-Frame particles could remain in close proximity to each other, when the concept of a doubled-up I-Frame using muons in each of three positions was considered. Due to the close proximity of positrons and electrons within the I-Frame it was considered extremely unlikely that such a closely-bonded particle would work. However, with careful consideration it would appear that there should be a balance point where the forces of attraction and repulsion would level out. Taking the example of a neutron and proton, how this would work is shown below, in principle (caveat: the drawing below is 2 dimensional, and should be taken as a close approximation to demonstrate the principle, which could well need to be considered in at least 6 dimensions for a proper analysis or simulation).
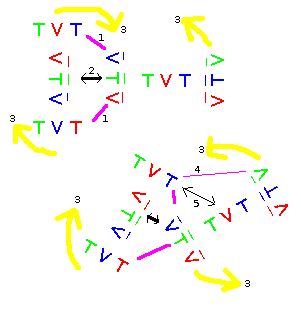figureShowing a neutron and proton stably rotate in close proximity
|
Walking through this diagram, the quarks are shown with three colours (phases) identified with Red, Green and Blue on a proton (left) and neutron (right). Attraction between proximate quarks is shown in purple (1). Repulsion shown in black (2). Direction of rotation about the central quark in each I-Frame shown in yellow (3).
So as the neutron and proton align at 90 degrees to each other, one outer down quark of the neutron comes into close proximity to the central down quark of the proton. Assuming a square law of attraction and repulsion, the down quarks repel each other (2) whilst simultaneously the down quark is attracted to the two up quarks at the ends of the very same proton (1). This seems at first consideration to be paradoxical and an arrangement ill-equipped to produce stability (the nuclear force), but considered purely from a mechanical perspective, amazingly it actually works.
As the two particles rotate, the repulsion and attraction remain in play, but now, additionally, one outer up quark of the proton begins to come into proximity with the inner up quark of the neutron as well as the other outer down quark of the same. So as this occurs there is a less strong repulsive force (5) betweeen two up quarks, as well as a less strong attractive force (4) between two up and down quarks, both of which become stronger as the other down quark rotates away from the proton, resulting in its paradoxical dual repulsive and attractive forces being lessened. Obviously, by the time the two particles reach a 45 degree rotation from their original starting point, all those forces become equal. Another 45 degrees later the positions are reversed, and that quadrant of the cycle will have been covered. In this way the two particles remain in an extremly closely-linked interlocking and stable relationship.
The exact details of the relevance of the colour (phases) is as of yet unclear, but is suspected to result in a coherent phase-locked loop that keeps the "spin" of the outer triplets in absolute synchronised lock-step with the rotation of the neutron and proton's rotational cycle.
One important question arises: how can the two opposing forces of attraction and repulsion result in the "nuclear force"? In other words, why do the neutron and proton remain in such an amazingly-stable orbit at a constant distance away from each other? Consider the mechanics of the arrangement shown by the forces (1) and (2). If the force is a simple square law, then if the two down quarks become too close together, the repulsion (2) would simply push them apart. With the two attractive forces (1) being further away they are less effective. However, should the distance between the particles become larger, the two attractive forces (1) would exceed that of the repulsive force (2), resulting in an overall attraction.
Thinking of this purely in mechanical terms that would allow an actual physical and practical demonstration:
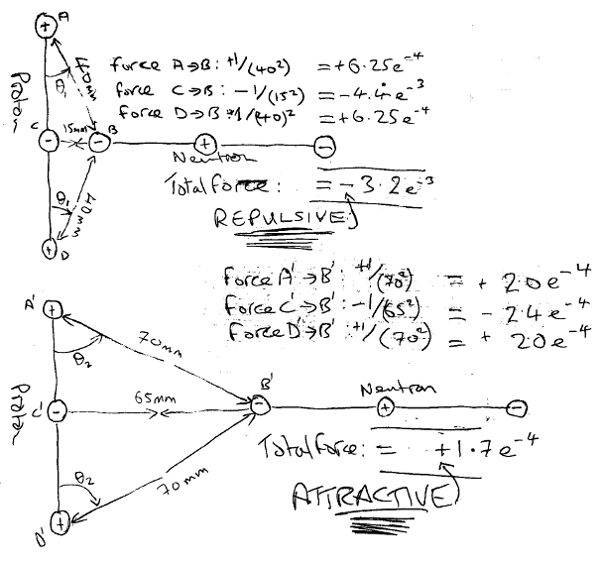figureIllustrating the repulsion and attraction resulting in "Strong Force"
|
In this illustration there is a proton with an up quark at A and D, and a down quark at C. There is also a neutron with a down quark at B. The top diagram has the neutron and proton close together; the bottom diagram has them further apart.
Here it is clear that in the top diagram, the sum of the inverse-square-law forces (A-B, C-D and D-B) when the neutron's down quark is close to the proton's down quark, results in a net total (repulsion), and yet at distances slightly further away, as shown in the bottom diagram, the sum of those exact same forces is a net total (attraction).
So it is quite interesting to note that this would actually result in some harmonic oscillation - "ringing" - where individual neutrons and protons would continuously bounce back and forth around a happy medium. That central point could approximately be calculated - ignoring other effects such as centripetal force, and only taking one group of triplets into account at a time - by sin(angle) * 2 = cos(angle). Or, more specifically, if as suspected a square law is involved:
1/sqrt(sin(angle) * 2) = 1/sqrt(cos(angle)).
A quick http://lkcl.net/reports/rishon_model/angle_search.pypython script and one iterative search later shows this angle to be approximately 26.6 degrees, no other quarks taken into consideration, no centripetal forces or other factors. In other words: below 26.6 degrees between the line of the outer up quark of the proton and the outer down quark of the neutron and there is a repulsive force keeping the proton and neutron apart, whilst above 26.6 degrees the balance turns the other way and there is a net attractive force.
It is anticipated that examining a more comprehensive version of this equation with respect to the distance between the proton and neutron would result in a derivation of the nuclear force. Factors to take into consideration in deriving such would include:
Interestingly, the frequency of Rishon waveform oscillation is unlikely to be involved in the above. Relativistic effects however might have to be taken into consideration.
The above is quite involved. It first requires a model of the relationships of the forces between Rishons: without that it would be challenging at best to get the model to work. However, if the underlying model of Rishon particle force relationship were correctly ascertained (Clifford Algebra being at the top of the list), then deriving the Nuclear Force using the above considerations as the basis would be a clear validation of the whole Extended Rishon Model.