Expanded Rishon Model Particles

In the Rishon Model [1] there are two types of particle: T and V. However the original lacks an explanation for generations, as well as a satisfactory analogy as to why T and V should exist. Piotr Zenczykowski provides a mapping to the Standard Model [2] through O(6) phase space using Clifford Algebra. We take a different perspective, that all particles are photons obeying Maxwell's equations and that Rishons are a record of the phase of the photon, in real and imaginary numbers, at key points on the photon's track. (We note in passing that Clifford Algebra is a generalisation of complex numbers).

We begin from a base model of a massless synchotronic photon in a phase-locked loop [4]. This being the case, all photons having phase, polarity as well as frequency, T may be considered to be the "real" mathematical part of a photon's polarity and V may be considered to be the imaginary part. From known physics covering photons we therefore already have the mathematical tools necessary to describe the Rishon Model: all that was missing was the identification.

Under current investigation is both String Theory as well as the old model of toroidal "knots" as the basis for elementary particles. A 3,2 toroidal knot would have the required characteristics of having three points at which phases would peak, as well as inherent spin 1/2 [3] [4]. Three peaks give the opportunity to express one each of T and V particles, as well as giving an explanation for "colour" as being - quite literally - three phases (of the same photon). Also useful for visualisation purposes is Sundance Bilson-Thompson's topological Model [7] (note however that Bilson-Thompson begins with the Rishon Model but assigns V a neutral charge with no explanation as to why). Also noteworthy is that toroidal knots come up in String Theory. So the possibility of "Vohu" being imaginary polarity therefore definitely feels like it is along the right lines.

The elementary particles of the Rishon Model are shown in Figure  1:

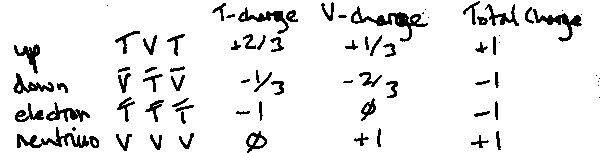figureFundamental Rishon particles and charges

From the perspective of a particle literally being a photon, the sum total of both the T-charge and V-charge of each of the Rishons must be either +1 or -1. Considered thus: three points, 120 degrees apart, on a sine wave must, by definition of a sine wave, exist, period.

figure3,2 (Trefoil) Knot, marked with three phases R, G and B

We see in figure 2 three separate colours: these correspond to the three "opportunities" at which T or V may be expressed. As the polarity is permitted to rotate (from real to imaginary) as the wave progresses on its phase-locked loop, at each of these three places if the polarity is real we have T, and if it is imaginary we have T. The eight permitted patterns (if anti-particles are also included) is therefore defined mathematically by the limited possible polarisation options of the photon. So although it is possible to have TTV, the fact that the three Rishons are circularly linked (last back to first) TTV is effectively equivalent to both VTT and also TVT. We therefore use the convention of placing the differing Rishon in the middle (TVT, VTV).

In effect then, the Rishon Model is (just as in Sundance Bilson-Thompson's braids method [7]) simply a topologically convenient way to visualise particles. As such we explore Rishon generations within this easily visualised manner and note some surprising discoveries along the way.