Decay Patterns as Phase Transitions

Firstly, the concept of decay has to be dropped and replaced with the concept of "Phase Transformations". If particles may be viewed as standing wave circular photon patterns (a sine wave with phase and polarity), then particle "decay" of sine waves resulting purely and simply in... more sine waves with new phase and new polarity. Therefore to explain particle decay, we need nothing more than... more T and V particles. Kazuo Koike considers this same concept [5] (figure 3, "exchange of $T\overline{V}$ pair"): we extend it further, from the perspective of all three of conservation of energy, charge and phase being ultimately critical and fundamental:

Nature does not permit energy to come out of thin air without a perfect counterbalance (anti-particle). That includes intermediary particles.

These are the allowed phase transforms. To conserve energy, charge, and phase, they must occur in pairs (one $V\overline{T}0$ and one $\overline{V}T0$). In some phase transition diagrams the matched pairs we name "$VT*$" for convenience.

     $V\overline{T}0$ -> any pair may transform into any other pair of
                $\overline{V}\overline{T}\overline{V}$ + $VVV$
        or:     $\overline{T}\overline{T}\overline{T}$ + $VTV$
        or:     $\overline{T}\overline{V}\overline{T}$ + $\overline{V}\overline{T}\overline{V}$
        
     $\overline{V}T0$ -> any pair may transform into any other pair of
                $\overline{V}\overline{T}\overline{V}$ + $\overline{V}\overline{V}\overline{V}$
        or:     $\overline{T}\overline{V}\overline{T}$ + $TTT$
        or:     $\overline{V}\overline{T}\overline{V}$ + $VTV$

In essence, any pair from say the $V\overline{T}$0 group may transform into any other pair from the same group (including to the same original pair). Using the XOR operator (exclusive OR) as a convenient moniker for sine phase differential it can be shown that in one group, two Rishons remain unchanged, whilst the remaining Rishons cancel out to sum total 0 charge in both T and V (hence the name VT0):

We illustrate this as:

     $\overline{V}\overline{T}\overline{V}$ XOR $VVV$ leaves one V and one anti-T
     $\overline{T}\overline{T}\overline{T}$ XOR $VTV$ leaves one V and one anti-T
     $\overline{T}\overline{V}\overline{T}$ XOR $\overline{V}\overline{T}\overline{V}$ leaves one V and one anti-T
        
     $\overline{V}\overline{T}\overline{V}$ XOR $\overline{V}\overline{V}\overline{V}$ leaves one anti-V and one T
     $\overline{T}\overline{V}\overline{T}$ XOR $TTT$ leaves one anti-V and one T
     $\overline{V}\overline{T}\overline{V}$ XOR $VTV$ leaves one anti-V and one T

So the exchanges occuring in pairs ( $V\overline{T}0$ and $\overline{V}T0$ always occurring together which we name $VT*$ ) result in phase and polarity conservation (if all matter may be considered to be phase-locked concentric standing wave patterns). In diagrammatic form, considered from the perspective of each particle, these are the transformations that can take place:

figureChart showing the chain of permitted transformations

The only other rule is that the arrows in and out of these phase transforms may be applied in reversed time, in a Feynmann-like trick. Still under investigation (but considered extremely likely) is whether the number of time-reversals on phase transform pairs must also be conserved. i.e. if there are a total of 3 time-reversals on $V\overline{T}0$ transforms within a "decay", there must equally be 3 time-reversals on the $\overline{V}T0$ transforms as well.

The "ultimate time-reversal" on a matched pair of VT0 transforms results in particle creation in groups of four quarks at a time: two pions where the sum total energy (all charges, all phases / colours) always totals zero (including the gamma radiation needed to separate the two pions).

Also of note is that the concept of a "gluon" comes from when a pion's two quarks are simultaneously the input and output of a matched pair of VT0 phase transforms.

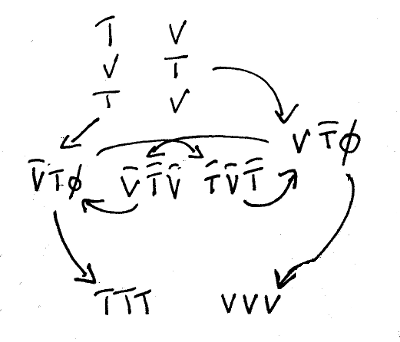figurePion phase-transition to positron (e+) and neutrino (ve)

What is happening in figure 8 is that each of the two quarks of the pion+ (top) undergo phase-transformations into positron and neutrino (bottom), but the energy to do so requires a balance. That energy comes from the simultaneous creation and destruction (centre) of a pion-, which acts as the dual simultaneous input and dual simultaneous output of both VT0 phase transforms. When a pion is created and then instantaneously destroyed in this fashion as an intermediary aid in phase transforms, the Standard Model gives it the name "gluon".